EXCELで有限要素法の強度解析（５） - シミュレーションのトビラ

2019/1/29 内容を全面的に書き直しました。

５．要素剛性マトリクス
- 片持ち梁の例
  - 微分方程式による解法
  - 積分(仕事とエネルギー)を用いた解法
- 外力を受ける物体の力の釣り合いを弱形式で表現する

５．要素剛性マトリクス

　さて、いよいよ各節点における変位を求めます。
　変位を求めるにはどのように考えたらよいでしょうか。まず、変位を求める方法の考え方について少し整理してみます。

片持ち梁の例

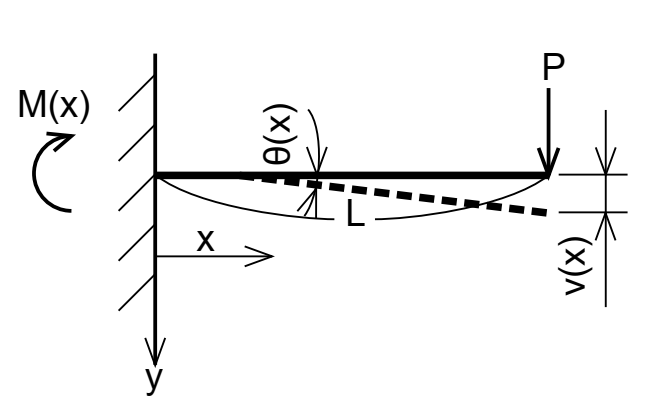
　構造力学において変位というと、例えば、先端に集中荷重を受ける片持ち梁の撓み量が挙げられます。
　理工系の学校に行かれた方であれば、一度は材料力学や構造力学の授業で解いたことがあろうかと思います。

微分方程式による解法

　力学の授業では、下図のようなモデルを用いて、任意の位置 $x$ における撓み量 $v_x$ を導出し、先端の位置 $x=0$ における撓み量 $v_0$ を求めたと思います。思い出してみましょう。

　この導出では、力の釣り合い式を立てるところからスタートします。外力と梁の反力が釣り合って梁が変形した状態で静止するわけです。
　外力 $P$ による位置 $x$ におけるモーメントを $M(x)$ 、材料のヤング率を $E$ 、断面二次モーメントを $I$ とすると、釣り合いの式は、
$\dfrac{d^2v(x)}{dx^2}=-\dfrac{M(x)}{EI}=\dfrac{Px}{EI}$
となります。 $v(x)$ を求めたいわけですが、二階微分の形になっていますので、積分を2回行うと、
$\begin{align} \dfrac{dv(x)}{dx}=\theta(x) &=\dfrac{P}{2EI}x^2+C_1 \\ v(x) &= \dfrac{P}{6EI}x^3+C_1x+C_2 \end{align}$
となります。ここで、 $C_1$ と $C_2$ は積分定数で、 $\theta(x)$ は撓み角です。
　境界条件として、位置 $x=L$ における撓み角 $\theta(L)$ 及び撓み量 $v(L)$ は共に0ですので、それぞれ代入すると、
$\begin{align} C_1 &= -\dfrac{PL^2}{2EI} \\ C_2 &= \dfrac{PL^3}{3EI} \end{align}$
となります。よって、任意の位置 $x$ における撓み角 $\theta(x)$ 及び撓み量 $v(x)$ は、
$\begin{align} \theta(x) &=\dfrac{P}{2EI}x^2 -\dfrac{PL^2}{2EI} \\ v(x) &= \dfrac{P}{6EI}x^3-\dfrac{PL^2}{2EI}x+\dfrac{PL^3}{3EI} \end{align}$
となります。以上より、先端位置 $x=0$ における撓み量 $v_0$ は、
$v_0 = \dfrac{PL^3}{3EI}$
と導出できます。
この微分方程式による解法であれば、あらゆる $x$ の位置における撓み量が求まります。

積分(仕事とエネルギー)を用いた解法

　ところが、上記の解法は、撓み量 $v(x)$ が2階微分可能な滑らかな関数でなければ解くことができません。数学的には $h$ →0のときの $\frac{f(x+h)-f(x)}{h}$ の極限値が、常に(全ての $x$ について)存在しないといけないことになりますが、これはかなり厳しい条件なのです。このように強い条件が求められることから、力学の分野では「強形式」と言うようです。
　一方で、一般的に関数は積分可能な場合がほとんどです。つまり、微分できる関数より、積分できる関数のほうが多いのです。
　そこで、上記の片持ち梁の問題を、積分を用いた方法で考えてみます。ここで利用するのが、仕事とひずみエネルギーです。
　物理学において、力と変位の内積を積分すると、エネルギーになります。上記の場合は、外力 $P$ が為す仕事 $W$ によって梁に蓄えられるエネルギー（ひずみエネルギー）がそれに相当します。

　まず、一般的な弾性変形する物体における仕事 $W$ は、

$\displaystyle W=\int^x_0 Fdx=\int^x_0 kxdx=k \left [\dfrac{1}{2}x^2 \right ]^x_0=\dfrac{1}{2}kv_x^2=\dfrac{1}{2}Px$
で表されますので、上記の片持ち梁の場合には、
$W=\dfrac{1}{2}P{v_0}$
と表すことができます。

　次に、ひずみエネルギー $U$ は、

$\displaystyle U=\int^L_0 \dfrac{M(x)^2}{2EI}dx = \int^L_0 \dfrac{P^2x^2}{2EI}dx=\dfrac{P^2L^3}{6EI}$ 　
となります。

　外力による仕事 $W$ が全てひずみエネルギー $U$ にかわるわけですから、

$\begin{align} W&=U \\ \dfrac{1}{2}Pv_0 &=\dfrac{P^2L^3}{6EI} \\ v_0 &= \dfrac{PL^3}{3EI} \end{align}$
となります。
　このように、仕事とエネルギーによる積分の形式を用いても、微分方程式による解法と同じ結果になります。

　ここで注意しなければならないのは、積分の形式による解法は、あらゆる $x$ の位置で満たすべき方程式を解いているわけではないということです。
　つまり、この解法では、特定の位置（上記の梁の場合は先端位置）の撓み量しか求めることができません。しかしその代わり、 $0→L$ という領域で積分できる関数であれば方程式を解くことができます。
　このように、微分方程式よりも関数に対する制約が弱いことから、力学の分野では、「強形式」に対して「弱形式」といいます。

外力を受ける物体の力の釣り合いを弱形式で表現する

　さて、本題に戻って、有限要素法で変位を求める場合を考えてみますが、メッシュを切ったことで、有限個の要素に分割されているとはいえ、それらが全部微分可能な関数で変位するかどうかわかりませんし、最終的に釣り合ったところの変位だけ求まればよいので、弱形式で解くことになります。流れとしては、力の釣り合い式（強形式）を導出し、それを仕事の式（弱形式）にします。

強形式を導出する

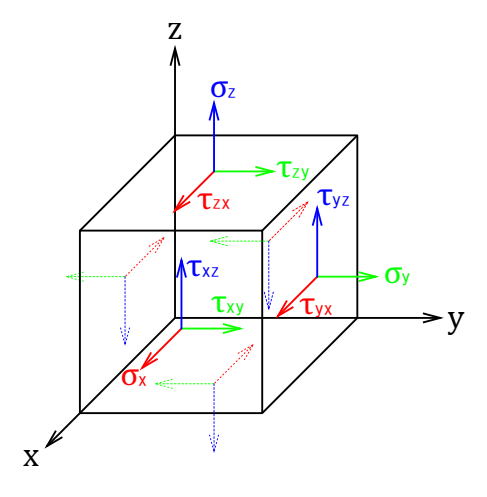
　まず、力の釣り合いを考えます。物体の内部に作用する応力は、応力テンソルの説明にあったように、下図のようになります。

　X方向を考えると、この直方体における垂直応力 $\sigma_x$ と、せん断応力 $\tau_{yx}$ 、 $\tau_{zx}$ が、X方向の外力と釣り合うことになります。外力は、物体内部に作用して応力を生じさせるもので、物体の体積や質量に比例することから、力学の分野では体積力 $b_x$ （または物体力）と言います。すると、力の釣り合い式は、
$\left( \sigma_x+\dfrac{\partial \sigma_x}{\partial x}\Delta x \right) \Delta y\Delta z + \left( \tau_{yx}+\dfrac{\partial \tau_{yx}}{\partial y}\Delta y \right) \Delta z\Delta x + \left( \tau_{zx}+\dfrac{\partial \tau_{zx}}{\partial z}\Delta z \right) \Delta x\Delta y \\ \hspace{100pt} - \sigma_x \Delta y \Delta z - \tau_{yx} \Delta z \Delta x - \tau_{zx} \Delta x \Delta y +b_x \Delta x \Delta y \Delta z = 0$
　これを $\Delta x \Delta y \Delta z$ で割ると、
$\dfrac{\partial \sigma_x}{\partial x}+\dfrac{\partial \tau_{yx}}{\partial y} + \dfrac{\partial \tau_{zx}}{\partial z} + b_x = 0$
となります。

　同様に、Y方向、Z方向についても立式してまとめると、

$\begin{cases} \dfrac{\partial \sigma_x}{\partial x}+\dfrac{\partial \tau_{yx}}{\partial y} + \dfrac{\partial \tau_{zx}}{\partial z} + b_x &= 0 \\ \dfrac{\partial \tau_{xy}}{\partial x}+\dfrac{\partial \sigma_y}{\partial y} + \dfrac{\partial \tau_{zy}}{\partial z} + b_y &= 0 \\ \dfrac{\partial \tau_{xz}}{\partial x}+\dfrac{\partial \tau_{yz}}{\partial y} + \dfrac{\partial \sigma_z}{\partial z} + b_z &= 0 \end{cases}$
　これが、力の釣り合い式（強形式）です。

仮想仕事の原理を用いて弱形式を導出する

　ここから、力の釣り合い式を弱形式にします。
　上記の力の釣り合い式は、X、Y、Zの3方向について連立した形となっていて、表記が煩雑なので、以下では、行列を使って一つにまとめた形で進めます。
　行列を用いて力の釣り合い式を書き直すと、

$\{ \partial \sigma \} + \{ b \} = 0$
と書けます。

　上述の片持ち梁の例で示したように、弱形式にするために、仕事の形にします。仕事にするには、外力（応力）ベクトルと変位ベクトルの内積を積分するんでしたね。
　しかし、変位と言っても、外力が変化してしまっては釣り合いが保てなくなってしまいますので、ここでは、外力が変化しないような無限に小さい変位を仮定し(仮想変位といいます)、 $\{u\}^T$ とします。
　積分は、3次元の立体的な物体を考えますので、物体の体積で積分することになります。すると、力の釣り合い式は、

$\displaystyle \int_V \left( \{ \partial \sigma \} + \{ b \} \right) \{ u \}^T dV = 0$
分解すると、
$\displaystyle \int_V \{ \partial \sigma \} \{ u \}^T dV + \int_V \{ b \} \{ u \}^T dV = 0$
となります。
　微分の形を消していきたいので、ここで、第一項を部分積分を用いて変形します。

部分積分の公式

$\displaystyle \int f(x)g(x)dx = f(x)G(x)-\int f'(x)(Gx)dx$

※ $G'(x)=g(x)$

$\{ \partial \sigma \} \{ u \}^T = f'(x)$ 、 $\{ u \}^T = G(x)$ として変形すると、
$\displaystyle \begin{align} \int_V \{ \partial \sigma \} \{ u \}^T dV &= \{ \sigma \} \{ u \}^T - \int_V \{ \sigma \} \{ \partial u \}^T dV \\ &= \int_V \partial ( \{ \sigma \} \{ u \}^T )dV - \int_V \{ \sigma \} \{ \partial u \}^T dV \end{align}$
よって、釣り合い式は、
$\displaystyle \int_V \partial ( \{ \sigma \} \{ u \}^T )dV - \int_V \{ \sigma \} \{ \partial u \}^T dV + \int_V \{ b \} \{ u \}^T dV = 0$
となります。
　まだ微分の形が入っているので、何とかします。ここで、第一項にガウスの発散定理を適用します。

ガウスの発散定理

$\displaystyle \int_V \dfrac{ \partial f}{\partial x}dV = \int_S f \cdot n dS$

※nは法線ベクトル
※体積積分が面積分に変わっている（物体の表面力による仕事に変わっている）ことに注意

すると、釣り合い式は、
$\displaystyle \int_S \{ \sigma \} \{ u \}^T \{ n \} dS - \int_V \{ \sigma \} \{ \partial u \}^T dV + \int_V \{ b \} \{ u \}^T dV = 0$
移項して、
$\displaystyle \int_V \{ \sigma \} \{ \partial u \}^T dV = \int_S \{ \sigma \} \{ u \}^T \{ n \} dS + \int_V \{ b \} \{ u \}^T dV = 0$

　次に、変位を方向で微分している $\{ \partial u \}^T$ は、ひずみに他ならないので、 $\{ \partial u \}^T = \{ \varepsilon \}^T$ とします。

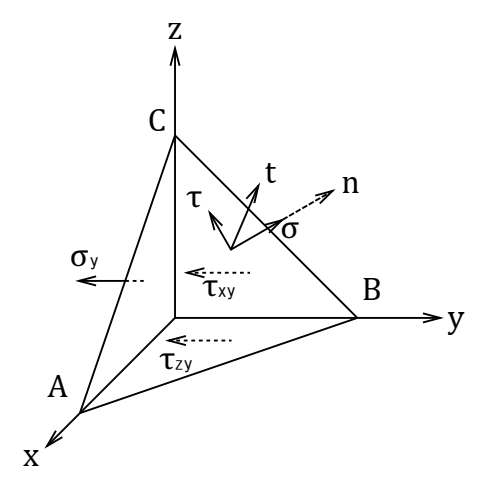
　更に、第二項にコーシーの関係式を適用します。
　コーシーの関係式とは、応力 $\sigma$ が働く状態にある微小部分を考えたとき、応力テンソル $\{\sigma\}$ と、任意の面に $\sigma$ に働く応力ベクトル $t$ とは、法線ベクトル $n$ を用いて、下記の関係があるという式です。これは物体のあらゆる部分で成り立ちますが、特に表面においては、応力ベクトルは表面に働く外力（表面力ベクトル）であり、それによって生じる応力テンソル $\sigma$ との関係を表すことになります。コーシーの関係式を適用することで、応力テンソルを含む第二項を、外力（表面力）による仕事を表す項にすることができます。

コーシーの関係式

$\{ t \} = \{ \sigma \} \cdot \{ n \}$

※{t}は表面力ベクトル

すると、釣り合い式は、
$\displaystyle \int_V \{ \sigma \} \{ \varepsilon \}^T dV = \int_S \{ t \} \{ u \}^T dS + \int_V \{ b \} \{ u \}^T dV$
となり、積分の形の式（弱形式）になりました。

　このように、力の釣り合いの微分方程式（強形式）に仮想変位を掛けて積分することで、仮想的な仕事の式（弱形式）にする原理を、「仮想仕事の原理」といいます。

要素剛性マトリクス

　上式の第一項は、ひずみと応力の内積なので「内部仕事」を表します。
　一方、第二項は表面力と変位（仮想変位）の内積なので「外部仕事」を表し、第三項は外部から作用する体積力と変位（仮想変位）の内積なので「外部仕事」を表します。
　ここで、右辺の第二項と第三項の「外部仕事」は、有限要素法では、要素の辺や綿に満遍なく作用している外力を、節点における集中力に変換して計算します。実際には、境界条件として節点に外力を設定する（または外力0を設定する）ので、右辺の式を具体的に計算することはありません。
　そこで、右辺の「外部仕事」を全て $\{f\}$ としてまとめます。すると、

$\displaystyle \int_V \{ \sigma \} \{ \varepsilon \}^T dV = \{ f \}$
となります。
　また、前回、前々回の記事で説明したように、BマトリクスとDマトリクスを用いると、
$\{\varepsilon\}=[B]\{u\} \\ \{ \sigma\} = [D] \{\varepsilon\}$
でしたので、
$\displaystyle \begin{align} \int_V \{ \sigma \} \{ \varepsilon \}^T dV &= \int_V [D] \{ \varepsilon \} \{ \varepsilon \}^T dV \\ &= \int_V [B]^T \{u\}^T [D] [B] \{ u\} dV \\ &= \int_V [B]^T[D][B] = \{ f \} \end{align}$
となります。
　ここで、
$\displaystyle \int_V [B]^T[D][B] = [ K_e ]$
として、さらに移項して整理すると、
$\displaystyle [ K_e ] \{ u \} - \{ f \} = 0$
となり、すっきりします。この $[ K_e ]$ を要素剛性マトリクスと言います。
　この式は、節点変位 $\{ u \}$ と節点荷重 $\{ f \}$ の関係を表す基本式で、節点の数だけこの式が作られます。
　要素剛性マトリクスの $[ K_e ]$ の積分の中身は、全て定数ですので、定数を要素内で体積積分するということは、要素の体積（厚さ $t$ と面積 $\Delta$ の積）を乗ずることと同じです。
　従って、要素剛性マトリクスは、
$\displaystyle [ K_e ] = t \Delta [ D ]^T [ B ]^T [ B ]$
となります。
　これら節点ごとの要素剛性マトリクスから、モデル全体のマトリクス(全体剛性マトリクス $[ K ]$ というひとつの行列方程式を作成し、それを解くことで解を求めます。

前へ　４．Ｂマトリクス
 次へ　６．全体剛性マトリクス